XYZ - matematisk problemlösning
Summering
- XYZ-delen består av 24 uppgifter per högskoleprov.
- Testa dig eller öva gratis med XYZ-uppgifter, från gamla högskoleprov och exempel från VIP-utbildningen, med XYZprogrammet, Provpassgeneratorn och Högskoleprovtränaren.
- Du kan förbättra ditt resultat på XYZ-delen på bästa sätt genom att studera som VIP-medlem.
Delprovet XYZ testar matematisk problemlösning och består av 12 uppgifter per provpass och alltså 24 uppgifter per högskoleprov.
Rekommenderad provtid är 12 minuter och den rekommenderade medeltiden per uppgift är därmed 1 minut per uppgift.
Till varje uppgift finns fyra svarsalternativ varav endast ett är rätt.
I denna provdel ska du lösa matematiska uppgifter. De områden som är inkluderade är aritmetik, algebra, geometri, funktionslära och statistik.
Officiell exempeluppgift
Linjerna ££ L_1 ££ och ££ L_2 ££ skär varandra så att vinkeln ££ x \neq 90 ^{\circ} ££. Vilket svarsalternativ är med säkerhet korrekt?
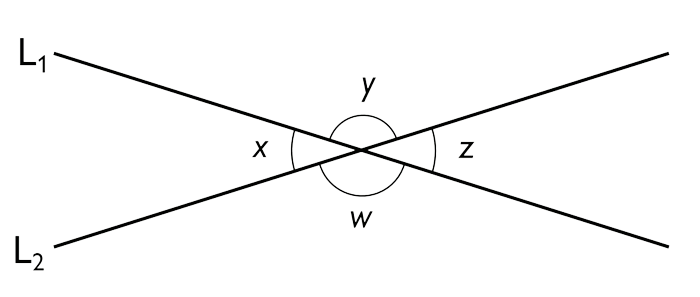
- ££ x + z = 90 ^{\circ} ££
- ££ 2x + y - z = 180 ^{\circ} ££
- ££ y - x = 90 ^{\circ} ££
- ££ 2w + z - x = 180 ^{\circ} ££
Vi ser att vi har två linjer som skär varandra vilket enligt reglerna för detta innebär att vinklar som är mittemot varandra, så kallade vertikalvinklar, är lika stora. Det innebär att
$$ x = z \\ y = w $$
Reglerna ger också att vinklar som är bredvid varandra, så kallade sidovinklar, har vinkelsumman 180°. Det innebär att
$$ x + y = 180 ^{\circ} \\ y + z = 180 ^{\circ} \\ z + w = 180 ^{\circ} \\ w + x = 180 ^{\circ} $$
Vi får i den inledande informationen också veta att x inte är lika med 90°. Med denna information ska vi nu avgröa vilket svarsalternativ som "med säkerhet är korrekt" och som alltid stämmer.
Vi tar ett svarsalternativ i taget.
Svarsalternativ A stämmer om t.ex. ££ x = 45 ^{\circ} ££ eftersom
$$ z = x \\ z = 45 ^{\circ} $$
varmed
$$ x + z = \\ 45 + 45 = \\ 90 ^{\circ} $$
Dock stämmer det inte alltid och t.ex. skulle x kunna vara 50° eller 12°. Vi kan därmed stryka svarsalternativet.
Svarsalternativ B kan vi skriva om genom att ersätta z med x eftersom
$$ z = x $$
Vi har då
$$ 2x + y - z = 180 ^{\circ} \\ 2x + y - x = 180 ^{\circ} $$
Vi kan subtrahera bort ett av de två x:en och kvar har vi då
$$ 2x - x + y = 180 ^{\circ} \\ x + y = 180 ^{\circ} $$
Detta stämmer med regeln för sidovinklar som ger just att x och y har summan 180°. Svarsalternativ B är således korrekt och vi behöver inte räkna vidare eftersom det alltid endast är ett svarsalternativ som är det korrekta.
Om vi har tid över på slutet eller vill kontrollräkna uppgiften kan vi också undersöka svarsalternativ C och D.
Svarsalternativ C beräknar vi genom att först konstatera att y och x är sidovinklar med summan 180°.
$$ x + y = 180 ^{\circ} $$
Vilket ger att
$$ y = 180 ^{\circ} - x $$
Ersätter vi y i svarsalternativet med detta uttryck får vi
$$ y - x = 90 ^{\circ} \\ 180 ^{\circ} - x - x = 90 ^{\circ} $$
Räknar vi vidare ser vi att x måste vara 45° för att svarsalternativet ska stämma.
$$ 180 ^{\circ} - 2x = 90 ^{\circ} \\ 180 ^{\circ} - 2x - 180 ^{\circ} = 90^{\circ} - 180 ^{\circ} \\ -2x = -90 ^{\circ} \\ 2x = 90 ^{\circ} \\ x = \frac{90 ^{\circ}}{2} \\ x = 45 ^{\circ} $$
Eftersom x kan vara både större och mindre än 45° stämmer inte alltid detta svarsalternativ.
Svarsalternativet D kan vi skriva om genom att ersätta z med x och subtrahera bort x.
$$ 2w + z - x = 180 ^{\circ} \\ 2w + x - x = 180 ^{\circ} \\ 2w = 180 ^{\circ} $$
Vi kan sedan beräkna att w måste vara 90° för att ekvationen ska stämma.
$$ 2w = 180 ^{\circ} \\ w = \frac{180 ^{\circ}}{2} \\ w = 90 ^{\circ} $$
För att w ska kunna vara 90° måste däremot även x vara 90° eftersom de är sidovinklar.
$$ x + w = 180 ^{\circ} \\ x + 90 ^{\circ} = 180 ^{\circ} \\ x = 180 ^{\circ} - 90 ^{\circ} \\ x = 90 ^{\circ} $$
Den inledande informationen ger dock att x inte är 90° varmed detta svarsalternativ aldrig stämmer.
Mer information och öva gratis
I VIP-utbildningen går vi igenom samtliga provdelar mer i detalj och du får unika strategier, genomgångar, tips och trix samt lösningsmetoder för alla tänkbara uppgifter som kan komma på provet.
Du kan testa dig eller öva gratis med XYZ-uppgifter, från gamla högskoleprov samt exempel från VIP-utbildningen, i våra olika övningsfunktioner. Även det senaste provets uppgifter finns tillgängliga.
XYZprogrammet Provpassgeneratorn Högskoleprovtränaren
Tack till HP guiden och till min coach som stöd för mina studier mot läkarlinjen. Utan er hade det inte gått! Jag gick från 0.95 (0.6 på verbala och 1.3 på kvant) till 1.75 (1.5 på verbala och 2.0 på kvant). Jag är så otroligt lättad och tacksam.
VIP utbildningen på HP guiden har så otroligt många bra funktioner för att underlätta studierna. Mina favoriter är bland annat "all matte du behöver" vilket ger dig enkel tillgång till allt du behöver repetera för att sätta 2.0 på kvantitativa proven.
 Coacherna på Högskoleprovguiden
Coacherna på Högskoleprovguiden
